Clauses in sentences result in relations between objects. If there is only one clause in a sentence, or several connected through coordinate conjunctions, the result is passed up to DiscourseSentence, to be connected to the sentence logical link (an attribute of the sentence object).
There will often be logical control or other connection, the relations needing to be connected together in a way that is specific to the clausal conjunction.
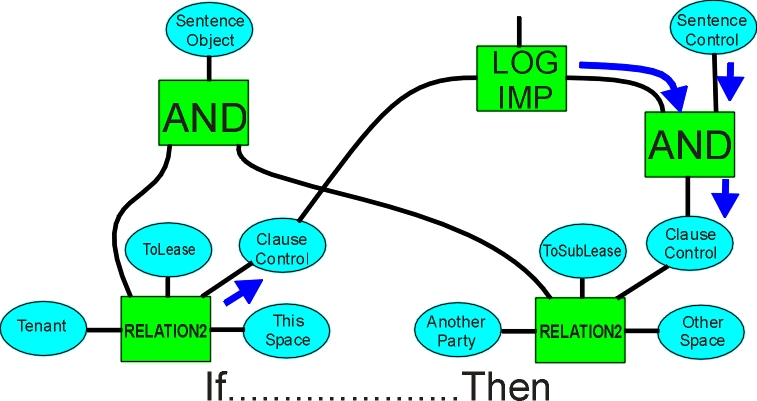
If Clause Then Clause

This is the classic definition of implication - an inverted AND operator. Assuming the sentence is true, then a true coming from the antecedent clause sets the consequent clause true, while a false from the consequent sets the antecedent clause false (with a LOGIMP to clean up the other cases).
The LOGIMP operator serves two purposes – it prevents a True from the consequent coming back and setting the antecedent True while it allows a False to pass, and it allows connection among multiple causes. If the number of causes is known, and all other causes are False, then the remaining cause must be True. If the connection is If and only If, then the LOGIMP is not inserted in the structure.
Nonexistence of the sentence sets the clauses nonexistent too.
The actual map
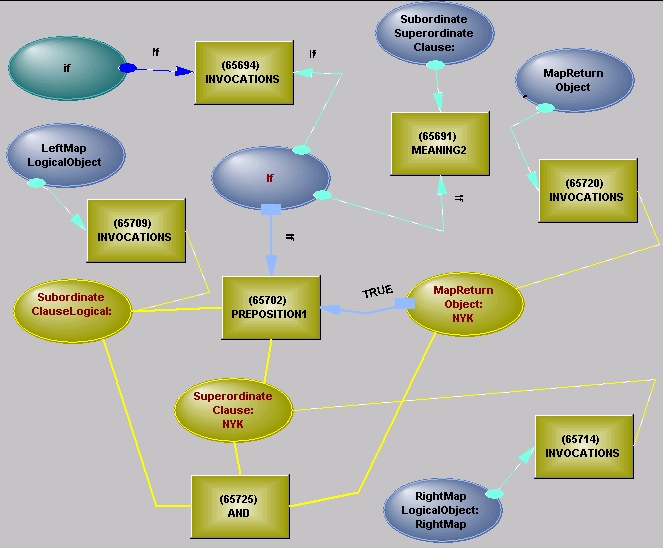
A If B
This uses a similar map, reversed in its parameters.
A As B
A occurs within the time period for B – set up connections between start and finish dates of the relations accordingly
It started raining as we drove north.
A When B
One event occurs at the same time as the other. The actual arrangement depends on whether the relation providing the timing is instantaneous or has duration (making it similar to "as")
Fred starts work when John finishes. (an instantaneous relation)
Fred eats when John eats.
A Whenever B
One event occurs at the same time as the other, on each occasion the other event occurs – an implied causal relation, not just coincidence.
Fred works whenever he can.
A Where B
A location is taken from another relation.
Fred searched for gold at the place where the river widened.
Not A Unless B
B is a necessary condition for existence of A
It cannot happen unless John makes a mistake.
This is If and only If using a negation to state it.
A Until B
The finish date of one relation matches the start date of another relation
Keep taking the medicine until you feel better
Once
The start date of a relation matches the end date of another
Payment is required once the goods are delivered.
Although, Though, But...Still
A cause overridden
He went there although he had been warned of the danger.
He had been warned of the danger but he still went there
Insofar As
A cause of limited validity
Insofar as he could ascertain, the ice on the lake was safe.
Each of the above clausal relations is expressed by maps, which connect the logical, existence or other attributes of relations together in ways specific to the individual clausal conjunctions. The maps are similar to those used for prepositions, but here the maps specify what element of each relation they require - logical object, existence object, etc.
Where the number of causes is known (and is greater than one) the outputs of the LOGIMPs can be connected together to force one of the causes to be true (or change its probability if there are still several choices).
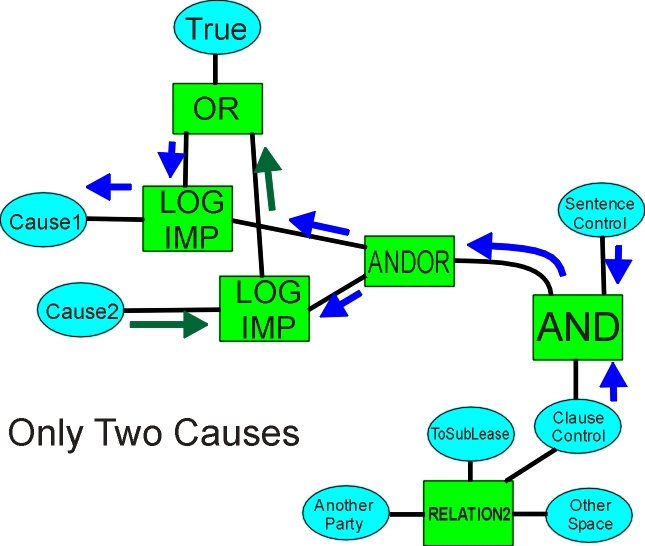
Here, the consequent is known to be true, and Cause2 is false. The modelling assumes there are only two causes, so the other cause must be true. If there is still the possibility of an unknown cause, it can be connected to the OR and given a low probability, pushing up the probabilities of the causes which are not known to be false. If the ANDOR receives a True on one of its inputs, it does not radiate Trues to the other inputs - it acts as an OR in one direction, an AND in the other.