Dynamic Constraint Reasoning for Prepositions
Abstract
Many areas of language have ambiguity, and use of prepositions is one of the most fluid. A method of using a map to set up a dynamic constraint reasoning problem is described. Various means of constraining the problem are shown, including inheritance, relations, relation parameters, propositional and existential logic, and values, at various removes. If the initial constraint reasoning, using only the existing connections and states, succeeds, the map attempts to actualise inherited structure, or build new structure, which may cause an inconsistency and failure. Similar maps are used to build logical connectives. The method is a combination of pattern matching and constraint reasoning, and can be used to join any complex cognitive objects together, where the method of connection is dependent on the objects and their surrounds.
Introduction
A system has been set up to read quasi-legal text and build the structure that the text represents [1]. The system sits on an underlying constraint reasoning system (UCRS), which operates mainly in build mode. The structure being built has logical and existential states, objects and relations, where relations are objects. What is typical is that islands of structure are built, and then need to be linked in complex ways. Prepositions are one example of several areas where constraint reasoning is used in building the structure. A specialised constraint reasoning system has been constructed to handle prepositions. It is specialised in that it only propagates sets of objects and logical states – numeric operators such as LESS are responsible for building ranges from the numeric objects they are given. The UCRS is intended for interactive entry of declarative statements and uses logical or object equivalence operators to link the statement structures to a logical spine. This would be wasteful if used for structure that is to be repeatedly built and which is more efficiently described graphically, thus eliminating the need for spinal connection. Also, the links in the specialised system carry directives – Match, Actualise, Build, Merge, and Replace. Match requires an operator to match sets of objects in its links against its semantics, Actualise implies Match but also builds the structure if it is only inherited, Build builds the structure without any attempt at matching unless an inconsistency intervenes or it already exists. It is not uncommon for the same structure to be built at two different places – Merge or Replace causes them to become one (when it is realised that Fred Bloggs and the milkman are the same object, they are merged). A null set presented to most operators (not Object OR) represents an inconsistency. The map operates on a hypothetical basis – all changes are stored, and if an inconsistency occurs, the map reverts to its original state and signals failure. If no inconsistency occurs, the build directives in the map are used to build the new structure, and the map is cleaned for reuse. Immediately after building, any active states are propagated into or out of the structure. The map can be operating within a higher level hypothesis set up by the UCRS – even if it succeeds, all that it has built can be undone if the relative plausibility of several alternative higher level meanings is being examined.
Preposition Application
There are about one hundred prepositions or preposition-like objects in the English language, and some of them have up to fifty meanings. Some meanings are reasonably general – the "up" of "Jack and Jill went up the hill" – while some are very specific – the "percentage of" of "3% of the drugs". Some prepositions double as logical connectives, "for" or "as", for example. Some prepositions are tightly coupled with verbs as collocations, although not necessarily, and it can take considerable subtlety to discriminate between a collocative use and a normal use. Noun phrases and the Germanic possessive form use the same mechanism, and are treated as though there were a virtual preposition – ‘The security guard" or "the guard’s security".
Active Map
A map is created which describes a possible pattern of connection between two or more complex objects, and the constraints applying for that connection to be valid. Some parts of the connection are simple and direct, while others require considerable propagation of states or objects within the constraint network. The various methods of applying constraints are described below.
Inheritance
Inheritance is represented in the system by using a network of INVOCATION and MEMBERS operators, each of which has a logical control. PARENT and CHILD operators are used in the map to verify inheritance, with cutting of sets depending on the logical state of the control. The inheritance state will be evaluated if the control is left unknown, and transmitted if it resolves to true or false. Evaluating inheritance is not as simple as it may seem. Some objects carry baggage, in that they, or their ancestors, may carry a Nochild operator, indicating that they are not a child of a particular ancestor, even though their immediate ancestor is. All objects are also words, so there is an automatic Nochild of Word on all objects while resolving parentage in maps. Sometimes ambiguity needs to be resolved in the inheritance chain, based on the properties of the object. Inheritance can also be computable – "part of the building is on fire". The "of" couples some of the properties of the building to "part", but not all, not the indivisible properties such as street number for example. Also, we may need to go down as well as up to find a link – "The gun’s magazine jammed" – not all guns have magazines. We may need to cross link, in that one object may be either the child or the parent of the other object.
We can say something must be either a child of A or B by the structure shown in figure 1 (The figure suggests that A and B are fixed objects, but they can also be propagatable sets of objects).
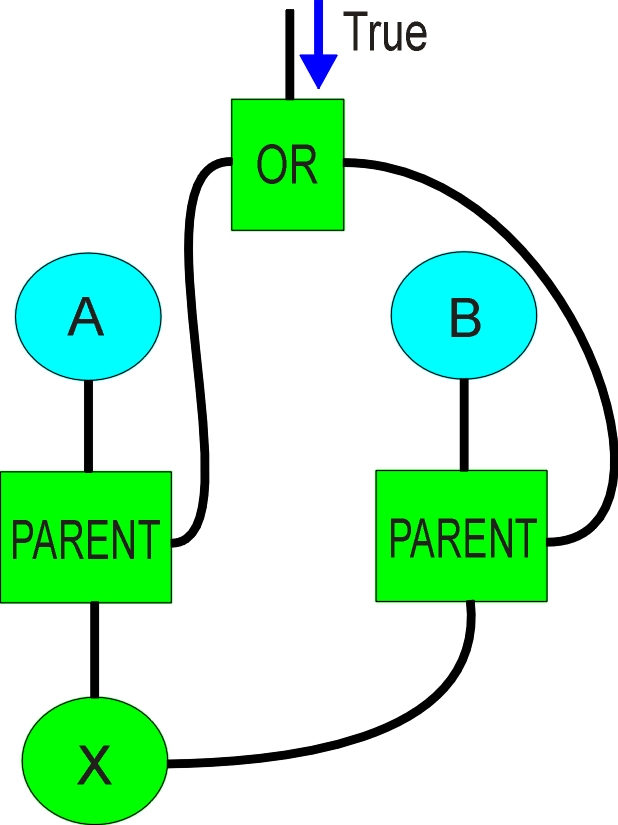
Figure 1. Using inheritance to control matching
When the set of objects arrives at X, it propagates to the PARENT operators. If no member of the set X is a child of A, then a logical False will propagate out of the PARENT operator shown on the left using the UCRS, then arrive at the OR, resulting in a true propagated to the other PARENT. When the set arrives at the operator, all members of the set that are not children of B will be pruned and the set returned to X. As shown, the mechanism would work poorly if neither control connection resolved to true or false – an object OR on two object sets could be used instead.
Value
Let’s say we have a requirement that a value of an attribute of an object should be less than 10 metres. The sort of structure we would have is shown in Figure 2 (the dotted lines indicate several levels of inheritance).
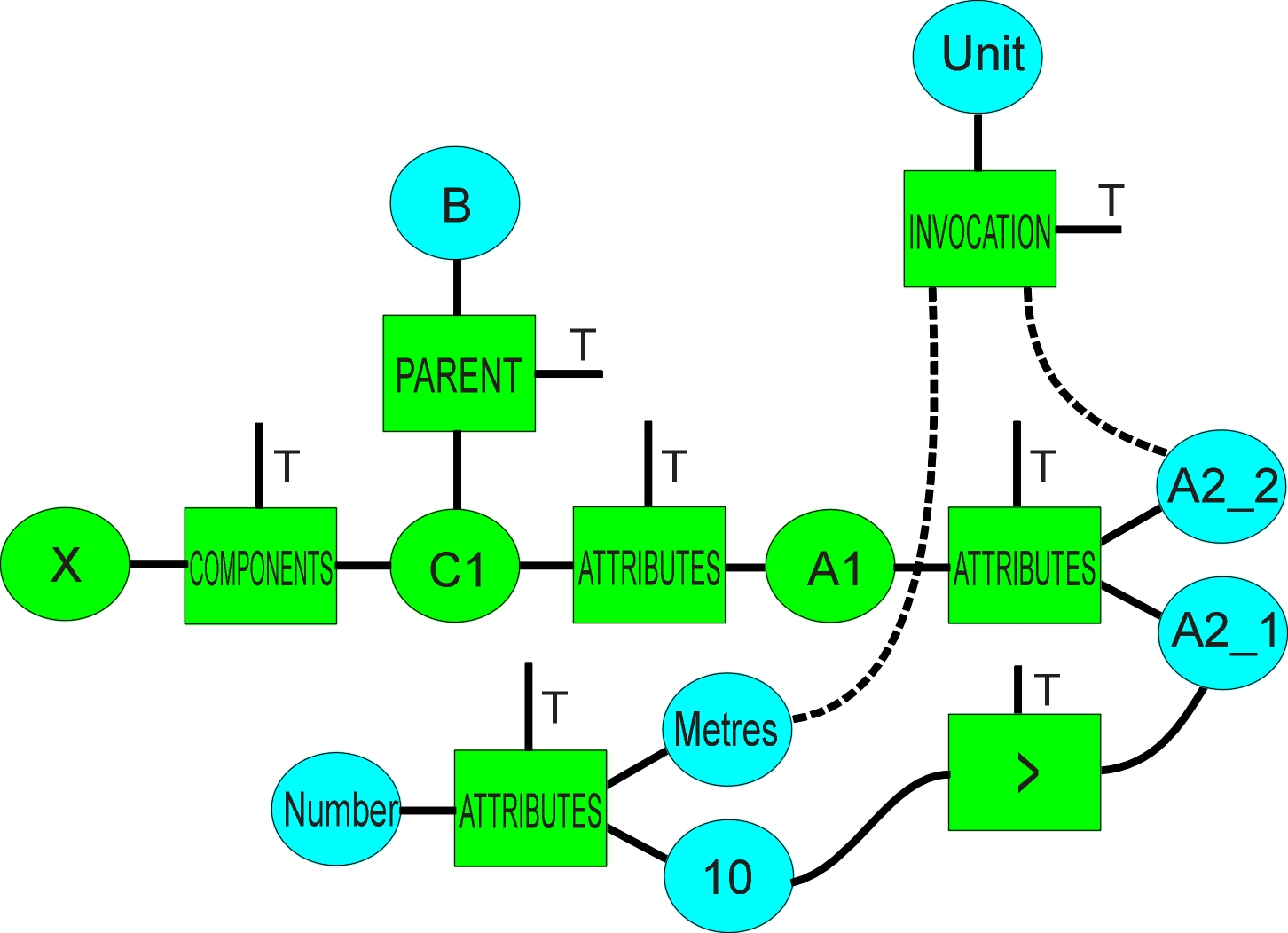
Figure 2. Using values to control matching
The map shown in figure 2 finds all of the direct and inherited distinct components of the members of set X, and uses inheritance from B to strip off the components we are not interested in at C1 (the set of components was propagated out of C1 on both links – the ordering of the links is irrelevant, if sometimes a little wasteful). It finds the attributes, one of which may be a measure (a value and unit). A set of numeric variables arrives at one side of a LESS operator. The operator does an automatic unit evaluation, discarding any area or other measures and converting to metres if necessary (using an operator which links to all linear units). If the set of objects is cut, it is propagated back along its path, changing any other sets in the process, which may then propagate outwards on other paths.
This construction may look hugely complicated compared to the usual constraint handling for numbers, but in typical scientific or legal text, numbers play an insignificant part in the web of constraints – perhaps about 1%.
Another way of using values is to encounter a Push directive in a link. The numeric (or range or string or list...) value is pushed into the surrounding structure using the UCRS, where it will encounter a much larger repertoire of operators than is necessary for prepositions. If no inconsistency occurs, the value is acceptable to the rest of the system. If a range or a list, it may have been cut, which would cause pruning of the source objects.
Relation Parameters
Many relations have multiple base forms ("he ran in a race" - intransitive, "he ran a business" - transitive) and these base forms have defined parameters. Controlling the parameters of the relations associated with the map allows us to control which base form is applicable to the map.
Existential or Logical State
All objects, including relations, carry an existential state and relations carry a logical connection (objects have a logical state too, but it is more to do with propagation on the logical substrate). It is easy to set up a relation and assert the existential or logical state (we admit to using a closed world assumption on existence – if existence is asserted in the map to be false, and we can’t find an instance of the relation or an equivalent relation or an inference of existence, we assume it is false).
Relational Chain
Relations can form chains with other relations
"He thought he needed to exercise the option to extend the loan"
and the map needs to be able to represent those chains and control what is acceptable at each step along the chain, including their parameters, their states and their temporal limits.
Integration
All the methods described integrate tightly together, the common currency being a set of objects propagating through the structure along the links. Occasionally, an object is prepared at one location and placed at another – the Replace directive cuts out one object and patches in another.
Complete Map
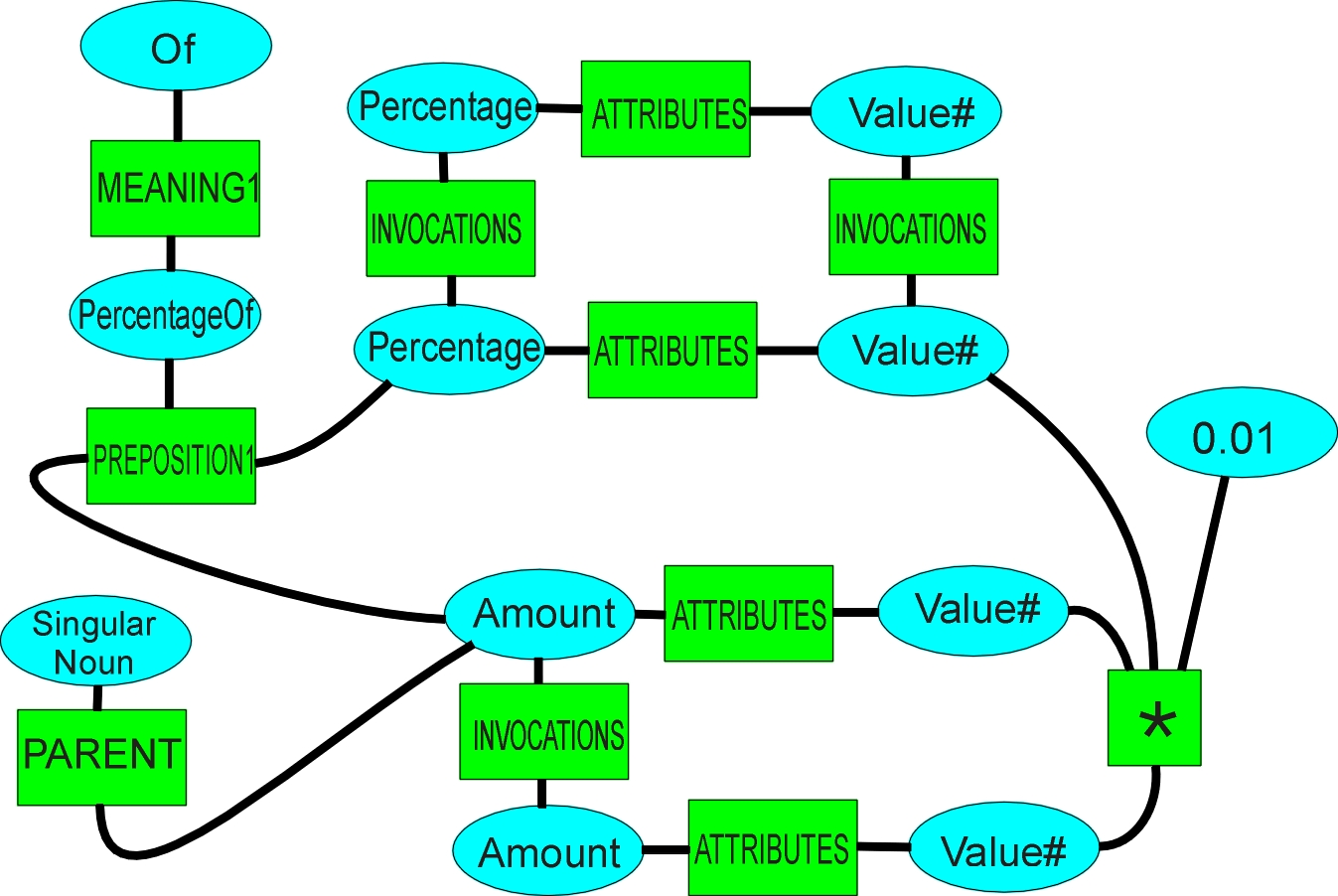
Figure 3. Map used for "3% of the amount"
The map shown in figure 3 would be found by searching around the "of" dictionary entry. The initial checks on its parameters would pass (the name of the map has no significance), and it would then be used for "3% of the amount of drugs...". It would build a new object, and set its amount value to 0.03 of the initial amount (building a multiply operator so the amount can be determined dynamically), the new object directly inheriting all the other properties of the initial amount of drugs.
Example Prepositions
We will use "by" as an example of the sorts of "parameters" a preposition may have.
The house by the lake
– location is an attribute of an object – the location of the house is linked to the location of the lakeThe man was shot by the robber
– provides subject for passive verbAn option exercisable by written notice
This is a little more complicated – only a person can exercise an option, so attempting to make "written notice" the subject of the ToExercise relation will fail. The "by" here is short for "by means of", or "using", a different preposition. So the fragment becomes
An unknown person can exercise the option by means of a written notice.
Use is one of the trickiest things a preposition does –
He cut the rope with a knife
is transformed into
He used a knife to cut the rope
where ToUse is a three connection relation (a causative verb).
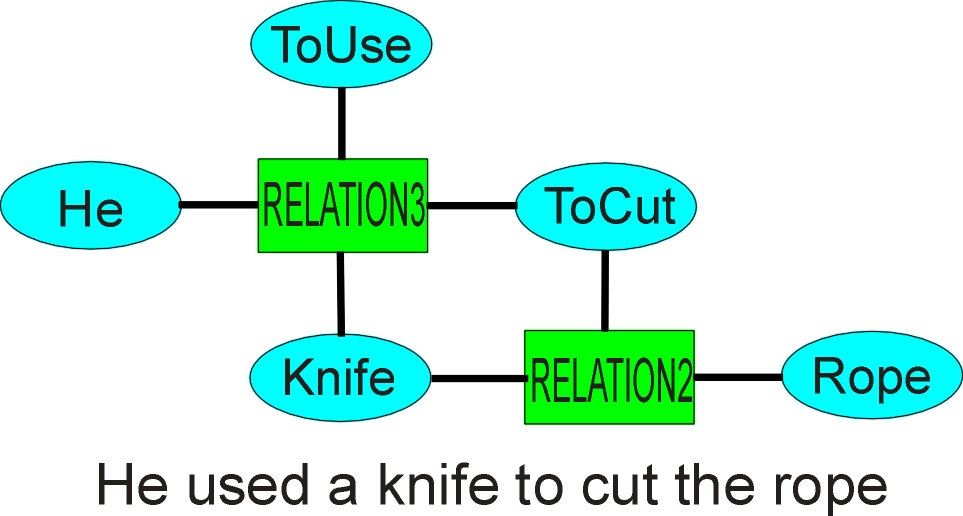
Figure 4. Preposition "with" inserting a relation
To create the structure in figure 4, the map will need to cut connections – "He cut the rope" would already have been built by the clause builder – and insert a new ToUse relation. Knives cut, but care doesn’t, so "He used care to cut the rope" requires a different construction – "He exercised care while he cut the rope", giving us simultaneous parallel relations.
Many prepositions share maps to keep the total down– "the dog of Fred" and the Germanic possessive form – "Fred’s dog", for instance, where swapping the parameters allows the same map to be used.
Map Sequence
Maps are arranged in sequence around a preposition object (the dictionary entry), with maps that will return true or false existence encountered first. In searching through maps, any that will return a true or false for existence will terminate the search. A map that returns true implies that it should be built immediately, without examination of further maps – the connection between the parameters by the preposition is so strong that it would never be deliberately broken by a jump in a chain (native speakers will break every rule, but we had to stop somewhere). A map that returns false implies that the connection is not possible and some other connection should be sought, usually by looking left in a chain. If several maps match, but do not return true or false, we need to wait for more information.
Chains
Another area where constraint reasoning is used in the system is in breaking up a long chain, which may include prepositionals, participials, conjunctions, commas, relative pronoun clauses. While this is a difficult area, it does have some strong constraints, such as sheathing, where objects over which connections have jumped are no longer visible to objects on the right of the sheather.
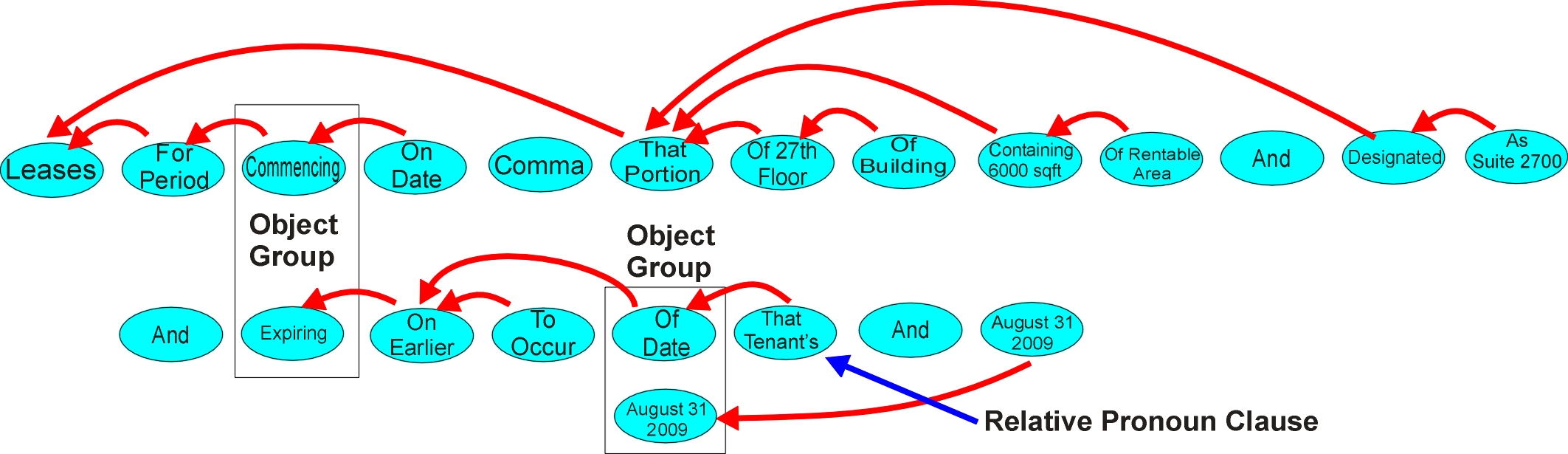
Figure 5. Textual chain
Figure 5 is an example where the operation of the prepositional maps is used to provide information to a higher level system, which is determining what parameters to pass to the prepositional maps as it seeks to break up the linear textual chain into clumps of context around objects.
Joining ClausesActive maps are also used as a general way of combining the rich variety of subordinate/superordinate and superordinate/subordinate clauses. Figure 6 shows a map for joining a subordinate If and a superordinate Then clause. An inverted AND operator is inserted, to represent exactly what logical implication implies (existence is handled separately).
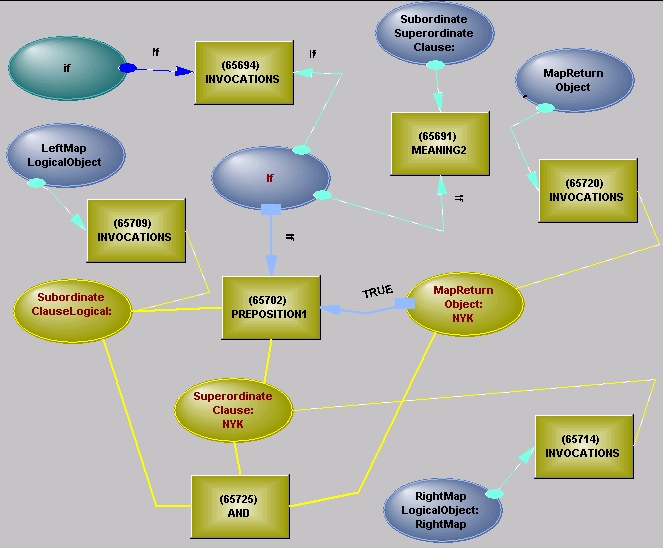
Figure 6. Active map used to join clauses
Conclusion
Active maps provide a useful specialisation on top of a more general constraint reasoning system. Using constraint reasoning allows a broader and deeper analysis of context around a preposition. The ability of the active maps to blend construction with constraint reasoning makes them both powerful and easy to specify and test. The ability to undo everything on failure allows for a match, speculative build, match, build approach. Their applicability extends beyond prepositions to many other places where complex cognitive objects need to be connected together in complex ways.
References
[1] Extensions to Constraint Reasoning