This description of NPV is based on the use of a flexible modelling tool, and is not relevant to
simplistic algorithmic tools like spreadsheets and financial modellers, with their
directed approach to analysis.
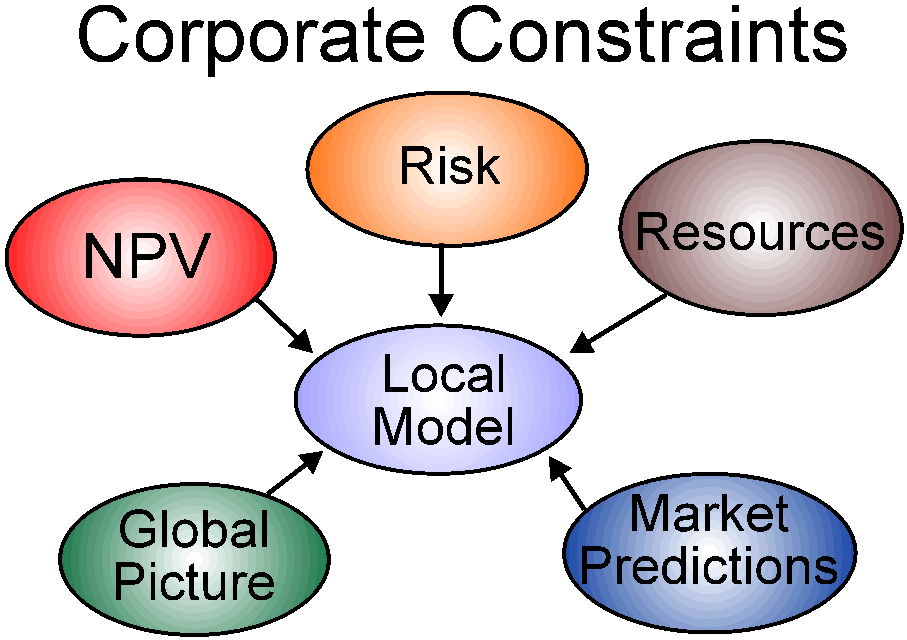
The people preparing submissions to head office for implementation of major projects would like to feel that their submissions meet corporate guidelines, but how to issue these in a flexible way.
Rather than having a rigid format and a list of goals to be met, a project template can be an active set of constraints which guide creation of the project model. Using NPV as an example:
NPV
is a simple way of determining the relative worth of a project by reducing the cashflow to
a single number. For an investment in a project, NPV is calculated on a cashflow which
will typically looks like the diagram, where all the variability has been stripped from
the project by making firm assumptions about where everything will occur, and the cashflow
in each period.
It may be more useful to allow some variability to remain in the scenario, to get bounds on the possible NPV to aid in making other related decisions. The resulting cashflow diagram shows variability of magnitude and risk of slipping. Without these being present, the person who interprets the NPV must look to other measures to assess the risk.
If a range is available for the NPV, it would then be useful to constrain the range, and have this feed back into the decision-making process. The minimum NPV may be a nonlinear function of the amount to be invested, making it a rate of return which is variable depending on amount to be invested. Other factors which may be included are time to payback and risk. The structure used to evaluate NPV is replicated over the time periods, and changes to amounts per period or interest rates can ripple in either direction through the structure. The person preparing the plan has a knob which constrains the NPV of the project, and in doing so, constrains the elements of the project. By twiddling the knob in combination with other controls, various alternatives (whether costs or times or plant process types) are forced out of contention.
An advantage of the undirected constraints approach is that corporate management can set a minimum NPV figure, and this will feed back into the planning model, constraining cashflows and timing of events. With some other metrics also acting as constraints (risk versus time, maximum exposure) and interacting with each other, the people developing the model are "directed"along the corporate path, and are much less likely to produce a good NPV figure based on invalid assumptions, assumptions that had to be made when there was no way of carrying variability forward in the analysis.
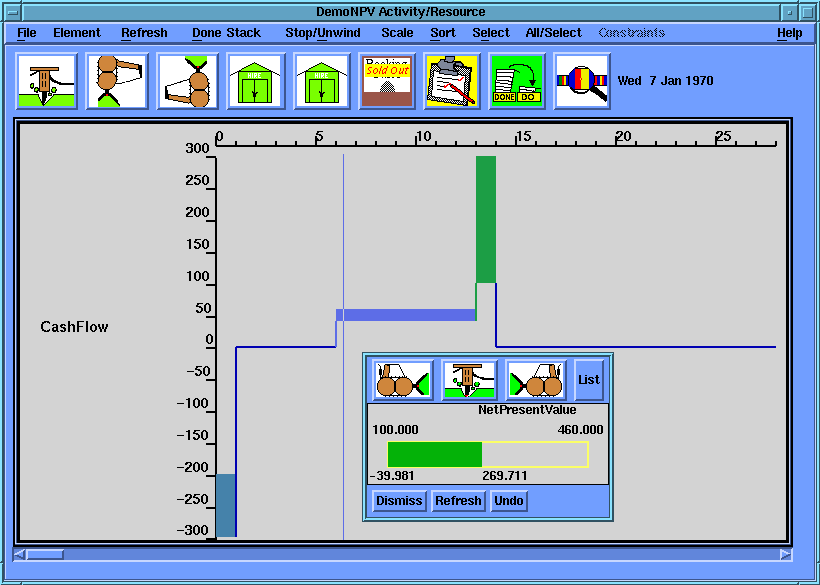The modelling environment presents the planner with a graphical representation of the
cashflow and activity positions, and allows constraints to be added and changed on the
cashflow, activities and the NPV so that the response of the plan can be studied. Note
that the bulldozers for cashflow constraints move vertically within a time period, while
moving horizontally in a time constraint fashion for activity starts. The small popup
constraints window permits adding constraints on non timebased elements of the model, such
as NPV. With multiple windows being simultaneously displayed and updated, the user can
change the NPV and see the cashflow and the activity starts move around in response to the
change.
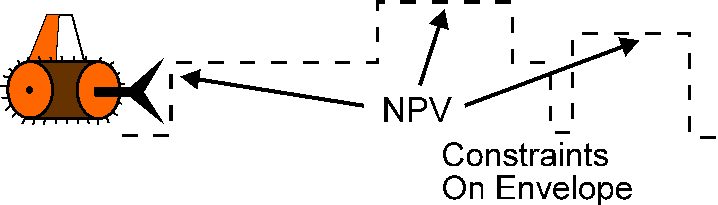The model allows more complex interacting constraints, such as a
link between Payout and EndValue, to be easily added, the effect observed, then removed.
In this way, users can train themselves in the operation of the model, adding additional
constraints if it goes outside the bounds of feasible operation.