Abstract
A knowledge network is an active analytic model of some complex state
or behaviour. The model has many properties that allow it to be used in design, high level
planning and scheduling. Undirectedness is the most important property, giving the
description a richness unobtainable by other means. The stackless operation of the model
allows for human interaction. The micro scheduling of its own activity means it is more
adaptable to the scheduling of modelled activities. Some operators used in planning and
scheduling models are described, as well as operators that extend the formalism into
non-analytic areas.
Introduction
This paper outlines the use of knowledge networks for high level
planning and scheduling. A knowledge network is intended to provide a generalised analytic
model of a problem area, and to allow all the inferences that may be drawn from such a
model. The network is made up of variables, operators and links, and has associated with
it a message passing mechanism. The operators are active elements which change the
information on any of their links in response to incoming changes on any of their links. A
link with incoming information can immediately become a link with outgoing information, so
operators can communicate directly with each other, and can change the topology of the
network as they do so.
The knowledge network implements various techniques that are necessary
for efficient analysis of scheduling problems, such as conversion of logical constraints
to equivalent numerical constraints where possible. Specialised operators to represent the
behaviour of tasks and usage of resources allow a compact description of the scheduling
model.
In comparison with the alternative algorithm/data structure approach,
the knowledge network, with its embedding of logic in an active model, is non-algorithmic.
Its lack of specialisation is a weakness only in simple problems, where a simple algorithm
can take advantage of the problem structure. Many people tolerate simple algorithms, and
hope that a layer of thought on top will result in a good outcome - instead, the simple
algorithm guides their thoughts as well, towards a simplistic outcome. The knowledge
network avoids the necessity for an algorithm and can be used to analyse complex problems
where the phasing of the decision-making is a large part of the problem..
Why a Different Approach
 Most scheduling tools are based around some form of algorithm, more or less
purpose-built, and rely on the operation of the algorithm matching (or "keying
into") the structure of the scheduling problem. This works well for static scheduling
problems, where everything is to be scheduled and the structure of the problem
doesn’t change over time, but such simple problems are rare in complex areas of human
endeavour. Sometimes a strongly mathematical solution, like linear programming, is deemed
adequate for the long term stable part of the problem, while the short term varying
aspects are ignored as being inconvenient. If a more applicable algorithm is required, it
may take months or years to develop, is marred by many hacks and patches, and is out of
date before it is implemented, due to changes in the process coming from new methods or
different behaviour of upgraded plant.
Most scheduling tools are based around some form of algorithm, more or less
purpose-built, and rely on the operation of the algorithm matching (or "keying
into") the structure of the scheduling problem. This works well for static scheduling
problems, where everything is to be scheduled and the structure of the problem
doesn’t change over time, but such simple problems are rare in complex areas of human
endeavour. Sometimes a strongly mathematical solution, like linear programming, is deemed
adequate for the long term stable part of the problem, while the short term varying
aspects are ignored as being inconvenient. If a more applicable algorithm is required, it
may take months or years to develop, is marred by many hacks and patches, and is out of
date before it is implemented, due to changes in the process coming from new methods or
different behaviour of upgraded plant.
There have been many efforts to improve the operation of scheduling
algorithms, with each new advance increasing the specialisation of the application, or
requiring the planner to be ever more inventive in attempting to twist the
algorithm’s behaviour to get the required result. Complex scheduling problems are a
mass of dynamic interactions, where decisions need to be made based on the current states,
and it is difficult to predict beforehand what those states will be, or create some rules
which apply to just that particular set of conditions.
A good criterion for judging scheduling algorithms is their
"scheduling granularity", what will they schedule down to. If large assumptions
are made as to the problem structure, the granularity can be coarse, leading to
efficiency, but anything not meeting the assumptions cannot be scheduled simultaneously -
it can't add two numbers together, because that was not in the assumptions of what it
would need to do. A Knowledge Network schedules at the atomic level of analysis - the
level of individual analytic operators - so everything can be done. More precisely, the
operators schedule themselves. It also doesn't schedule what it knows doesn't need to be
done, so it is not as inefficient as it might sound.
The Knowledge Network approach uses a Constraint Reasoning technique to
allow a much more realistic description of the scheduling problem. The description of the
problem in terms of its constraints and interactions provides the structure for its
analysis. If the process being scheduled changes, new constraints can be added which
directly represent the changes. Where many sub-problems are to be combined, each
sub-problem brings with it its own active logic, allowing reliable automated assembly of
the overall scheduling problem. Some scheduling problems have a "window" which
moves through time, revealing an unpredictable subset of tasks to be scheduled. Again,
this subset can be continuously and dynamically assembled into a scheduling model, the
assembly taking place through connection of the components of the tasks and new
information flowing as soon as connections are made.
 The knowledge network structure is initially undirected and can transmit tentative
information about possible solutions in any direction. There is no external algorithm
attempting to schedule while obeying the constraints. Instead, there is a scheduling
machine built out of the constraints and interactions that describe the behaviour of the
objects being scheduled. This is the Non-Algorithmic approach.
The knowledge network structure is initially undirected and can transmit tentative
information about possible solutions in any direction. There is no external algorithm
attempting to schedule while obeying the constraints. Instead, there is a scheduling
machine built out of the constraints and interactions that describe the behaviour of the
objects being scheduled. This is the Non-Algorithmic approach.
How Much is Different
What has been removed is the need for transformation of scheduling
requirements into the form of an algorithm and a data structure. The
major difficulty with that approach is the requirement to phase the operation of the
algorithm running on a sequential instruction computer so that the relevant states of the
process are examined at the appropriate time. This requires that the programmer has an
intimate knowledge of the process (and any possible future changes to the process), and
develop a mental model of the algorithm so that it may be written out in the form of a
program. A minor difficulty is that the data structure cannot describe activity, so all
necessary active logic must lie within the algorithm.
Once written and left for some time (weeks, months), the algorithmic
program is very difficult to change because the mental model the programmer used to
produce it has evaporated. Changes can now damage the fabric of the algorithm, because the
detailed understanding of the interactions woven into it has been lost. The notion of
weaving extends past the algorithm to encompass the data structure that the algorithm
operates on. Change to the data structure requires change to the algorithm, and vice
versa. The complexity that this leads to is shown by the requirement that the algorithm
anticipate every possible variation of the objects being scheduled, and their interaction
with other objects.
The Non-Algorithmic approach takes the descriptions of
the interactions and constraints, and directly creates a structure where they are still
evident (and individually identifiable). Changes can be made to the original description
at the business knowledge level. The most obvious difference between the two approaches is
the elimination of phasing by the programmer, the operators within the structure
controlling the phasing of information flow in the structure in response to changes at
their connections.
The non-algorithmic approach may seem inefficient, as it shuttles
information around the structure, but it is not "dumb". To use a related
example, the "natural order" algorithm that drives a spreadsheet is
quintessentially dumb because it attempts to schedule all calculations before it knows the
results of those calculations, and where the calculations might have led it. A
"dumb" algorithm requires "dumb" problems, or at least problems
strangled into a very constricted form.
The knowledge network could still be described as running an algorithm,
but it is an unusual one made up of operators, connections and the values within them.
There is no distinction between an algorithm and a data structure. Both are entwined
together, in a far tighter weave than a programmer could accomplish. The algorithm is
"inside" the problem description and observes the conditions at each operator,
rather than outside it with much less information to work on. A programmer has no direct
control over what occurs in the network, other than by altering the network structure or
the values that illuminate it.
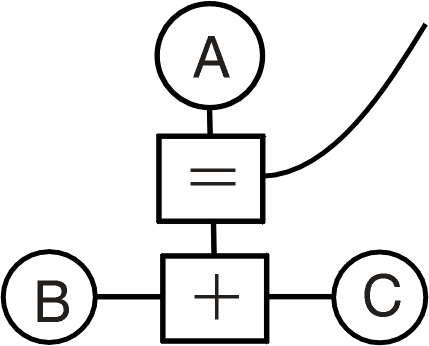
Undirected Interaction In The Network
The operators in the network are undirected - that is, they are capable
of handling information flowing in and out on any of their connections. A statement like
A = B + C
implies that the plus operator will maintain the truth of the relation
among A, B and C while the statement is operational, no matter which variable presents new
information about itself (note the logical control being exercised through the EQUALS. A
logical state can flow in or out from the EQUALS). The precise operation is that the
changed information moves along the link from the variable to the operator, the operator
gains control, examines the states and values on its connections, if necessary places new
information on any of its links or reports an error and then relinquishes control. If new
information arrives at a variable, all incoming information is compared for consistency,
and new information is sent out on all connections.
Taking a slightly more complicated relation,
IF A < B THEN C > D
information can flow into any of the variables, or into the logical
implication (IF) controlling the statement, or out of it (there is a control connection
for the statement, not shown in conventional textual forms, but assumed True). That is,
the statement may be driven True or False (effectively becoming IF A < B THEN C <=
D), it may drive its control pin, the consequent may negate the antecedent, or it may be
forced to be non-operable. Control of this constraint may have been exercised by another
constraint, so they can be layered without limit. The constraint statements are undirected
as to information flow, just as we should understand sentential logic.
As an aside, embedding constraints using the IF...THEN of computer
logic relies on building an entirely separate phasing mechanism to control the logic, but
to do so is a good way of strangling the scheduling problem by breaking it into
unconnected pieces.
The constraints use reasoning at the operators that make up the
constraints, rather than treating the constraints as black boxes, so many more inferences
are possible. Making the constraint statements behave as a human scheduler would
understand the logical interactions seems at least marginally useful in coping with
complex problems. If during scheduling a consistency error occurs, it occurs at a point
which is directly related to the problem description, not in the air (although, to be
fair, it may be necessary to chain back many links in the structure to find why the error
occurred where it did - not enough fuel is the same error as not enough range).
Operators like PLUS, LESS, IF have already been mentioned. Sometimes it
is necessary to embed non-analytic operators in the network. This can be done using
DISTRIBUTION and RELATION operators. The RELATION operator uses an adaptive graph to
describe the relation between two or more variables. The detail of the graph can be
obtained using Data Mining or other techniques, and can have its contents modified over
time by a learning mechanism. The DISTRIBUTION and RELATION operator has a Probability
control, allowing the outcome to alter depending on the probability obtaining during the
scheduling process. It is important to note that these operators sit at the same level as
every other operator, so propagating a range into the Probability control pin is no
different to propagating a number into a PLUS - the analysis is extensible, not segmented.
Efficiency Matters
The network operators tend to exceed what is understood by their
textual representations. The statement
A + B + C + D = E
is built with a single PLUS operator with multiple connections. The one
operator can see all the ranges that are pertinent to it, and make more inferences than if
three distinct but otherwise identical operators were used.
If a group of variables is to finally have an exclusive integer value
on each, it may be done by setting the group not equal to each other through a single
EQUALS operator, as
NOT EQUALS(List) - equivalent to NOT A = B
This is far more compact and efficient than thousands of statements
connecting every combination in a list of 50 variables (the infix operators can all be
used textually as functions with a list providing parameters, although
"function" is obviously a misnomer). Bringing the maximum amount of information
into focus at an operator maximises the potential inferences.
If there is a statement
IF A < 5 OR A > 10 THEN...
the logical OR is replaced with a numerical OR, combining multiple
logical scenarios into one numeric scenario with a range. If the consequents of an
IF...THEN...ELSE make multiple reference to a variable, as
IF A < 5 THEN B = 6 ELSE B = 10
then a structure is automatically created to enforce
B IN {6,10}
whenever the IF statement is true (the statement itself has a logical
connection) and before the value of A is known. The combination of techniques of network
compression and elaboration allows more powerful inferences to be made, stripping away the
impossible alternatives faster, important when designing or scheduling.
What Can Be Propagated
The network supports the propagation of logical states, numbers,
strings, objects, lists. Lists can include any type, including numeric ranges, network
structures, lists. Alternative values are supported, using the list transmission
mechanism. Numeric ranges can be discrete, such as 2,5, or integer 10..20, or real
1.4<->7.6, and may involve variables, such as A..B. Symbols are used, so 1..1000000
is transmitted as a single constant, not stored as a million bits. The ability to
propagate numeric ranges in symbolic form is essential for dynamic extensibility, the
variability in one part of the network being determined by another part. Probabilities
representing partially known logical states can be transmitted through the logical
connective operators in a Bayesian fashion, so scheduling under uncertainty is possible.
When the information to be transmitted becomes too complex to be
represented as a value or a list, activation is transmitted. That is, one operator signals
another by altering the environment and placing the other operator on the activation
queue. When the other operator gains control, it observes changes in its environment and
may place other operators on the queue. This technique is used to propagate distributions,
surfaces, resource/usage interactions.
Why Transmit Values
Some systems handling scheduling constraints use a method where ranges
are stored at the variables, with no linking network structure. The statements standing
for the constraints are parsed and executed, first with the minimum values and then with
the maximum values. For example, A = B + C could be used as a constraint. If a change
occurs at variable B, the statement is used to work out a new value for A, then turned
into C = A - B to work out a value for C. The method is simple, but has several negatives:
The equals sign has no meaning other than assignment to a location, so
there is no means of controlling the statement’s usability other than by external
means (a single layer).
The turnaround method falls over on those analytic statements which do
not permit rearrangement.
The turnaround method falls over if simple functions such as TRUNC and
MAX are used (so they can’t be used, compromising the problem description).
Complex analytic operators, such as the ACTIVITY operator connecting
Start, Finish and Duration, have no obvious turnaround form. They make sense in a network,
and may be conveniently represented in textual form as a function (although they are
functional on most of their connections).
Giving an operator control, even one as simple as PLUS, may allow it to
detect occurrences where inferences outside it may be drawn, based on the information it
has received from two or more directions. If operators do not have existence except as
instructions in program flow, then they are not going to make inferences.
The lack of logical connectives in a network structure militates
against the use of Bayesian logic in any integrated way.
The systems using the turnaround method require the problem to be
strangled into a form which suits the algorithm. Patches can allow a form of IF...THEN...,
but it is the IF...THEN of computing, the jump to a location, not the logic of scheduling.
Transmission of values through a structure, with computation occurring at the operators
and variables, removes these limitations, describes far more of the real problem, and
greatly increases the inferences that may be drawn.
Probabilistic Reasoning
Most times, design and planning must be undertaken with some
uncertainty. The logical connectives in the network can be made to provide Bayesian
behaviour in a way that is integrated with the operation of the rest of the network.
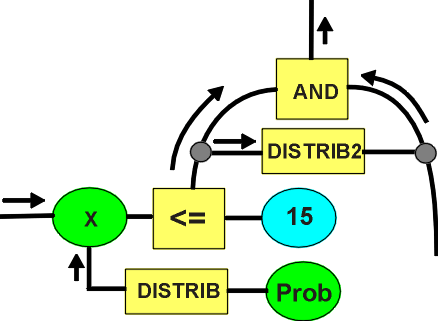 The
diagram indicates a network fragment of
The
diagram indicates a network fragment of
IF X <= 15 AND ...
Here, X has a distribution operator connected to it. The distribution
may be generated, such as Gaussian, or data mined. The distribution is stored in an
adaptive histogram, using ranges for compression in little used parts of the distribution.
When a change occurs to the range on X, the LESS THAN operator compares the current range
of X with the singular value 15 (it could be another range with another distribution) and
a probability in the range 0<->1 is transmitted in the logical connection. The AND
operator can make use of the two-dimensional distribution to determine the
cross-correlation. The probability can be moved into the numeric network for manipulation,
then moved back into the logical network again (Bayesian analysis has problems when used
in the large, rather than in toy examples. The network, with its ability to bring a large
amount of information to a focus, provides a framework for handling these problems).
Building Variability Into The Schedule
A good example of the rigidity of scheduling algorithms is that of the
Critical Path Method (CPM). The method works well where every task must be scheduled
within a resource limitation - erecting a skyscraper for example, where everything is
known in detail beforehand, and nothing is tentative or could be left out.. The method
works poorly in high level planning or a development environment, where the activities
themselves may be in a constant state of flux - even whether to do the project at all is
uncertain, and needs to be part of the analysis.
Alternative Activities

Planning at a high level often encounters the situation where one cannot
decide between two or more potential and mutually exclusive paths (something as simple as
which resource was last used, or perhaps different technologies to produce similar
outcomes). One path might be shorter but more expensive, or expose the plan to greater
risk of failure to complete some task. The logic deciding between the two paths can be
built into the network, and draw on as many influences as desired. The two alternative
paths can themselves be mini-schedules, and don’t need to have common starting and
ending points, as shown in the diagram.
Some activities in the plan may have risks associated with them - risks
that they may not occur, or that the duration becomes extended. There are two ways of
handling this, backup activities and contingent activities. The need for inclusion of
these sorts of activities can be determined based on a risk analysis also embedded in the
same network.
Backup Activities
Backup activities are worked on in parallel with the activity having
completion risk. The backup activity may take longer to complete than the minimum duration
for the main activity. However, if completion of the main activity does become a problem,
the work spent on the backup activity has been good insurance for keeping the overall
schedule on track. If the desired activity is completed, the backup activity is aborted.
Contingent Activities
Contingent activities can be embedded in the plan, ready to be
scheduled if failure occurs on some primary activity. As distinct from backup activities,
work on the contingent activity only begins when failure has occurred on the primary
activity. If the primary activity succeeds, the duration of the contingent activity is
forced to zero, rendering the activity nonexistent.
These specialised activities are not specialised operators, instead
they are assembled from the general purpose logical operators.
Method of Scheduling
When scheduling, there is usually a hierarchy of choices to make. One
can either make each choice in turn and then use branch and bound or similar techniques to
limit computation, or one can propagate the effects of a choice to reduce the number of
downstream choices - a technique called "forward cutting". The more initially
undirected the model, the more widespread can be the propagation (and the less
"forward" it appears, as the cutting may turn back on itself). As a result of
propagation, either the ranges of other variables are reduced, or inconsistencies are
encountered, forcing an immediate backtrack without wasted effort. This technique can
reduce the number of choices to be tried by a factor of thousands, making the optimisation
of complex planning models possible.
The backtrack in a knowledge network consists of restoring network
information changed as a result of the decision needing to be undone. Every part of the
network is made of the same "stuff" and every change (including changes in
network topology) can be backtracked, so backtracking is a seamless part of network
operation. One can make decisions, build "castles in the air" as a result, then
take them all to pieces again and try something else. Most other systems implement
backtracking by jumping out of a procedure which has a local copy of the variables. The
knowledge network backtrack uses a procedure to undo changes in the network - operation is
symmetric, allowing what is undone to be controlled as it is undone.
Scheduling must deal with many singular and awkward cases. Some
examples:
An ACTIVITY Lying In Wait
A task to be scheduled is represented in the network by an ACTIVITY
operator. The network can decide on whether a particular task is to be carried out by
switching its logical control pin. If an ACTIVITY operator does not yet have a TRUE or
FALSE state on its control pin, and it has a zero in its range of duration, it observes
any changes taking place on its Start and Finish pins. If the possible duration between
the Start and Finish values becomes less than its minimum real duration, the ACTIVITY
cannot exist, so switches its duration to zero and sends FALSE out of its Logical Control
pin. If connected through an XOR to another activity, the other ACTIVITY will switch TRUE,
forcing it to exist and be scheduled. The ACTIVITY operator has become a detector of its
own existence, by implementing undirectedness on its connections.
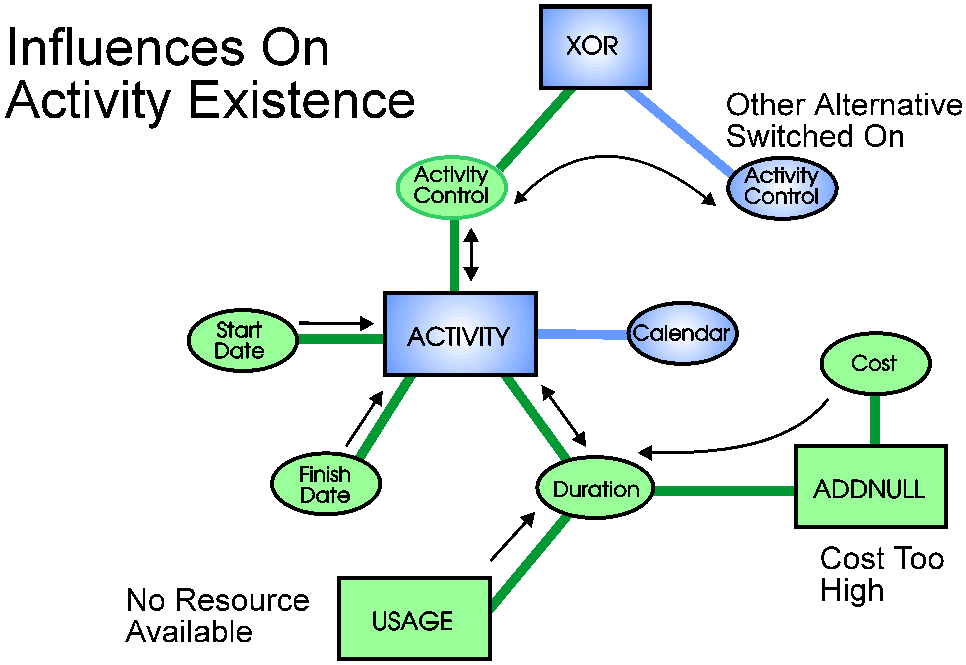
Tasks Swallowing Other Tasks
Heavy equipment usually has a preventative maintenance program, and the
aerospace area is obviously no exception. The larger maintenance tasks occur infrequently,
but if they need to be pulled forward for any reason, they should swallow smaller tasks
that would otherwise have been carried out separately. The logical control pin on activity
operators makes this modelling trivially easy to implement.
Piggybacking of Tasks
Some tasks should move to coalesce with other tasks that are in their
time range, but if the task on which they have piggybacked moves out of range, the task
must jump to another possibility within its range. This kind of logic is hard to build
into an algorithm, easy when active logic is built into the scheduling model.
The network activity resulting from the interaction of many renewable
and consumable Resource Usage operators, jostling with each other for resources and
continually reversing the information flows at their connections as the constraints
tighten, and the ability to control existence of tasks and turn resource usage on and off
from other parts of the network, provides a large part of the flexibility of the knowledge
network for scheduling applications.
Human Interaction with Scheduling
The handling of constraints is sufficiently flexible in a knowledge
network to allow constraints of arbitrary complexity to be added even during the
scheduling operation, while the other constraints are active and partial results are
already available. Constraints can be added textually or graphically. The added constraint
structure will immediately have values flowing in it from its points of connection to the
rest of the network, allowing its operators to modify those values. Unlike other
scheduling methods which are "stuck up their stack" and not amenable to user
interaction, the knowledge network method is essentially stackless, all the states being
represented in the network (and being accessible to connection).
Examples
No fully worked examples have been given in this paper, for the reason
that a knowledge network is a general method, and it is too easy to look at an example and
say "That is what it does", with the implication that is all it does. Examples
of use are spread over the spectrum of design, planning, scheduling and include -
scheduling of heavy maintenance of aircraft, ground movements of aircraft at an airport,
program management, project management of development projects, product design, financial
asset planning, marketing analysis.
Conclusion
The knowledge network approach to planning and scheduling has been
outlined. The knowledge network is intended as a general analytic tool, so it can describe
far more of the real problem than a tool dedicated purely to scheduling. Its area of
applicability is at the high level end of the spectrum, where uncertainty exists in what
is to be scheduled, or the objects to be scheduled must bring their specific behaviour
with them, being too complex to capture in a general purpose algorithm.
The knowledge network propagates relatively complex messages in a
relatively complex structure, making it much closer to the human scheduler’s
understanding of the scheduling problem. Its method of operation allows human intervention
during the scheduling process.
Bibliography
 Most scheduling tools are based around some form of algorithm, more or less
purpose-built, and rely on the operation of the algorithm matching (or "keying
into") the structure of the scheduling problem. This works well for static scheduling
problems, where everything is to be scheduled and the structure of the problem
doesn’t change over time, but such simple problems are rare in complex areas of human
endeavour. Sometimes a strongly mathematical solution, like linear programming, is deemed
adequate for the long term stable part of the problem, while the short term varying
aspects are ignored as being inconvenient. If a more applicable algorithm is required, it
may take months or years to develop, is marred by many hacks and patches, and is out of
date before it is implemented, due to changes in the process coming from new methods or
different behaviour of upgraded plant.
Most scheduling tools are based around some form of algorithm, more or less
purpose-built, and rely on the operation of the algorithm matching (or "keying
into") the structure of the scheduling problem. This works well for static scheduling
problems, where everything is to be scheduled and the structure of the problem
doesn’t change over time, but such simple problems are rare in complex areas of human
endeavour. Sometimes a strongly mathematical solution, like linear programming, is deemed
adequate for the long term stable part of the problem, while the short term varying
aspects are ignored as being inconvenient. If a more applicable algorithm is required, it
may take months or years to develop, is marred by many hacks and patches, and is out of
date before it is implemented, due to changes in the process coming from new methods or
different behaviour of upgraded plant.  The knowledge network structure is initially undirected and can transmit tentative
information about possible solutions in any direction. There is no external algorithm
attempting to schedule while obeying the constraints. Instead, there is a scheduling
machine built out of the constraints and interactions that describe the behaviour of the
objects being scheduled. This is the Non-Algorithmic approach.
The knowledge network structure is initially undirected and can transmit tentative
information about possible solutions in any direction. There is no external algorithm
attempting to schedule while obeying the constraints. Instead, there is a scheduling
machine built out of the constraints and interactions that describe the behaviour of the
objects being scheduled. This is the Non-Algorithmic approach.
 The
diagram indicates a network fragment of
The
diagram indicates a network fragment of
